每日公式之勾股定理
每日公式之勾股定理
数学公式:a² + b²= c²
勾股定理(Pythagorean theorem),描述了直角三角形中,直角边的平方和等于斜边的平方。其中,(a) 和 (b) 是直角三角形的两条直角边的长度,(c) 是斜边的长度。
在直角三角形中,如果一个角是直角(90度),那么根据勾股定理,直角边 (a) 和 (b) 的平方和等于斜边 (c) 的平方。表达式为: a² + b²= c²
例如,如果一个直角三角形的直角边 (a) 的长度是3,直角边 (b) 的长度是4,那么斜边 (c) 的长度可以通过勾股定理计算: 3² + 4² = 9 + 16 = 25 所以,(c² = 25),因此 (c = 5)。

这个公式在解决直角三角形相关问题时非常有用,也是数学中的基础内容。
在生活中,有时候我们需要找到合适的平衡点。勾股定理告诉我们,在直角三角形中,各边的关系是有规律的。类比到生活中,我们也可以通过找到平衡点,合理安排各方面的事务,使生活更加和谐。在面对问题时,有时需要换一个角度思考,就像在直角三角形中使用勾股定理一样,找到解决问题的适当方法。
mathematics formula: a² + b² = c²
This is the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse ((c)) is equal to the sum of the squares of the lengths of the other two sides ((a) and (b)). Here, (a) and (b) represent the lengths of the legs of the right-angled triangle, and (c) represents the length of the hypotenuse.
Specific explanation: In a right-angled triangle, if one angle is a right angle (90 degrees), then according to the Pythagorean theorem, the sum of the squares of the lengths of the legs ((a) and (b)) is equal to the square of the length of the hypotenuse ((c)). The expression is given by: a² + b² = c²
For instance, if the lengths of the legs of a right-angled triangle are (a = 3) and (b = 4), we can find the length of the hypotenuse ((c)) using the Pythagorean theorem: 3² + 4² = 9 + 16 = 25 So, (c² = 25), and (c = 5).
This formula is useful for solving problems related to right-angled triangles and is a fundamental concept in mathematics.
In life, just as in mathematics, finding the right balance is crucial. The Pythagorean theorem teaches us that in a right-angled triangle, there is a systematic relationship between the sides. Similarly, in life, we can achieve harmony by finding a balance and making reasonable arrangements in various aspects. When facing challenges, it's sometimes necessary to change perspectives, much like using the Pythagorean theorem to find the right approach in a right-angled triangle.
-

- 核心词汇buffet用法读音解析
-
2026-01-13 11:06:46
-

- 成都华阳
-
2026-01-13 11:04:32
-

- iPhone X正式发布:售价999美元64G起步,11月3日上市
-
2026-01-13 11:02:17
-
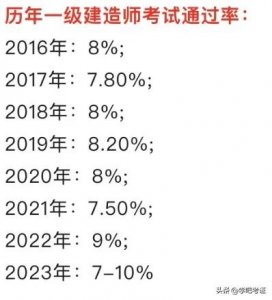
- 2024年一建通过率会是多少?
-
2026-01-13 11:00:03
-
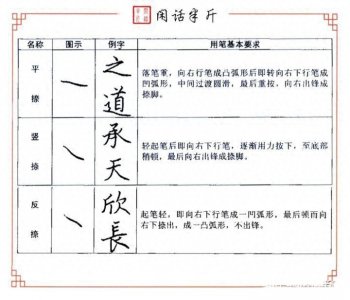
- 3.7、硬笔书法教程 | 笔画讲解——“捺”的写法
-
2026-01-13 10:57:48
-

- 于梓贝:两闯“好声音”,为了寻找自己的路
-
2026-01-13 10:55:34
-

- 微信和支付宝哪个更好?大数据告诉你,更多人都选择了它!
-
2026-01-13 10:53:20
-

- 南京应用技术学校怎么样?南京应用技术学校殴打学生真相
-
2026-01-13 10:51:05
-

- 立夏时节,芍药花开
-
2026-01-13 10:48:51
-

- 机动车左转怎么走?标准示范给你看→
-
2026-01-13 10:46:37
-

- 孩子们画的“移风易俗”宣传海报,超萌超可爱!
-
2026-01-13 10:44:23
-

- 保尔 柯察金的精神没有过时
-
2026-01-13 10:42:08
-

- “门前五包”聚合力 “温暖城管”见行动
-
2026-01-13 04:52:50
-

- 资中有“橙”意,4.8万吨血橙订单已被签约2024年资中血橙营销大会成功举行
-
2026-01-13 04:50:35
-

- 中国最矮的山—静山,海拔不到一米!网友:确定这不是小土坡
-
2026-01-13 04:48:21
-

- 越虐越美的多肉—金枝玉叶
-
2026-01-13 04:46:07
-

- 杏色究竟适合啥肤色的朋友们?
-
2026-01-13 04:43:52
-

- 谈一谈你对高价彩礼的看法
-
2026-01-13 04:41:38
-

- 伤愈复出的武磊,找回进球感觉需要时间
-
2026-01-13 04:39:24
-

- 泉州黄金海岸被海南“秒杀”!这些问题让游客失望透顶!
-
2026-01-13 04:37:09



 15本男主占有欲强的宠文小说推荐,《深渊女神》一生推
15本男主占有欲强的宠文小说推荐,《深渊女神》一生推 40岁以上的张惠妹长胖了,你知道为什么吗?
40岁以上的张惠妹长胖了,你知道为什么吗?